Systèmes géodésiques

Se positionner sur la Terre ou dans un environnement proche, géoréférencer, géolocaliser... Tous ces termes signifient attribuer des coordonnées à un objet dans un repère lié à la Terre. Un tel repère doit donc être défini, et le cas échéant complété d'une représentation de la Terre, pour qu'une action de positionnement puisse être menée. Cependant, l'expression des coordonnées est multiforme et il existe aujourd'hui un grand nombre de systèmes de référence de coordonnées, car la technologie et la législation évoluent !.
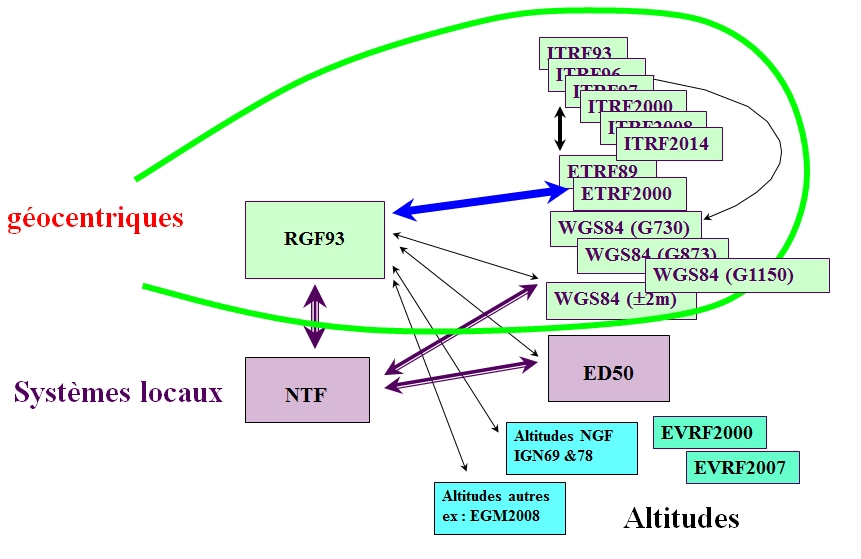
Repères de référence en métropole
Le nouveau décret sur les références est en vigueur depuis 2019.
Janvier 2021 : maintenance du repère RGF93
Système de référence terrestre
Le Système de référence terrestre international (ITRS) est le système de référence spatiale mondial idéal qui suit le mouvement diurne de la Terre. L'espace physique est alors 'considéré comme' un espace affine euclidien de dimension 3, tel que :
- L’origine O : proche du centre de gravité de la Terre
- L’axe OZ : proche de l’axe de rotation de la Terre
- OXZ : plan méridien origine
- OXY : plan de l’équateur
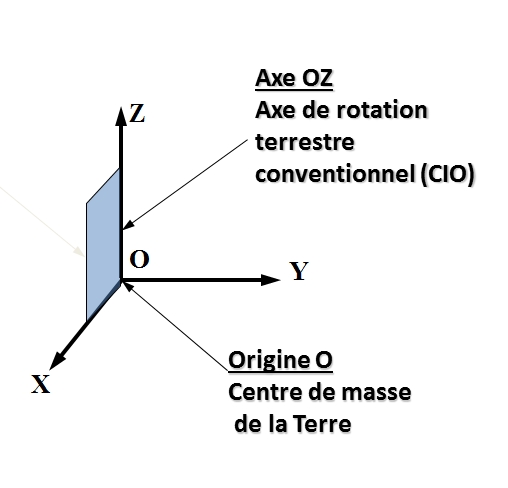
Système de Référence Terrestre
Chaque réalisation physique de l'ITRS est produite sous le nom de 'repère de référence' ou ITRF (International Terrestrial Reference Frame) pour chacun desquels on a choisi un trièdre repère affine. Chaque repère est un ensemble de points physiques avec des coordonnées déterminées avec précision dans un système de coordonnées spécifique. Ces coordonnées sont obtenues par la combinaison de solutions individuelles issues des techniques de géodésie spatiale : GNSS, VLBI, SLR, LLR et DORIS. Chaque technique utilise des réseaux de stations répartis sur l’ensemble de la Terre.
En avril 2022, l'IGN publie l'ITRF2020 qui s'appuie sur les observations de géodésie spatiale effectuées jusqu'au 31 décembre 2020. Cette nouvelle version de l'ITRF apporte des améliorations significatives par rapport aux précédentes réalisations : elle confirme l'estimation de la position du centre des masses de la Terre telle qu'elle avait été déterminée en 2016, mais fournit aussi ses variations saisonnières.
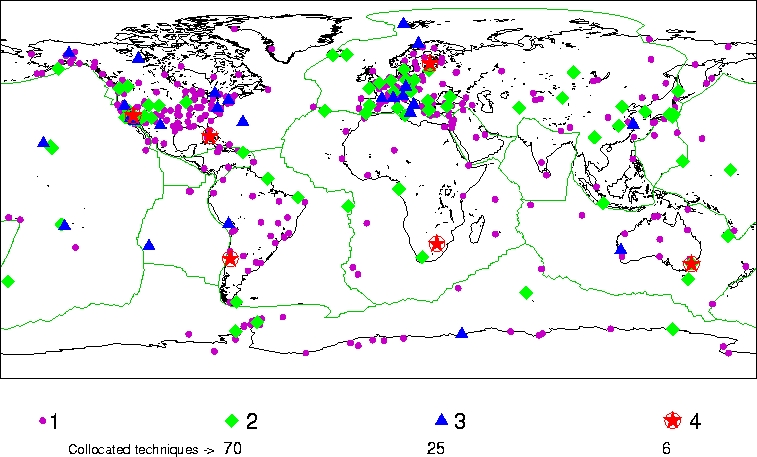
Réalisations de l'ITRS
Pour en savoir plus sur l'ITRF2020
Exemples de repères légaux au sens du Décret et de l'Arrêté en vigueur
- pour la métropole : RGF93
- pour les outre-mers : RGR92,RGFG95,RGM04,RGSPM06,RGTAAF07,RGAF09,etc...
Pour en savoir plus sur les textes de loi
Paramètres de transformation depuis l'ITRF2014 vers les références nationales

N.B. : Au XX° siècle, les coordonnées s'exprimaient dans des 'systèmes géodésiques', issus de techniques terrestres (Nouvelle Triangulation de la France, European Datum 50, Fort-Desaix, etc...) ou spatiales (WGS72,WGS84, NAD83, ..) On peut actuellement pour le calcul considérer ces 'systèmes' comme des repères de référence dans la mesure où existent les modèles de transformations de coordonnées
Ce ne sont toutefois pas des réalisations de l'ITRS.
Coordonnées cartésiennes géocentriques : X, Y, Z
Un point de la croûte terrestre est quasiment fixe dans un repère. Cependant, la position varie à cause :
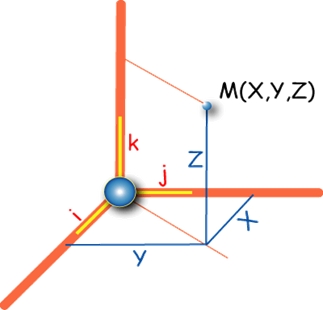
coordonnées cartésiennes
- de mouvements globaux
Tectonique des plaques (inférieur à 10 cm par an), rebond postglaciaire (quelques millimètres par an)… - de mouvements locaux
Séismes, glissements de terrain... - de mouvements périodiques
Marées terrestres (variations inférieure à 30 cm), surcharge océanique (variations inférieure à 20 cm), surcharges atmosphérique, hydrologique (variations centimétriques)
Un point M sera donc positionné par ses coordonnées et sa vitesse dans le repère à un instant (t)
M(t) = M(ti) + dM/dt *(t - ti) + ΣΔM(t)
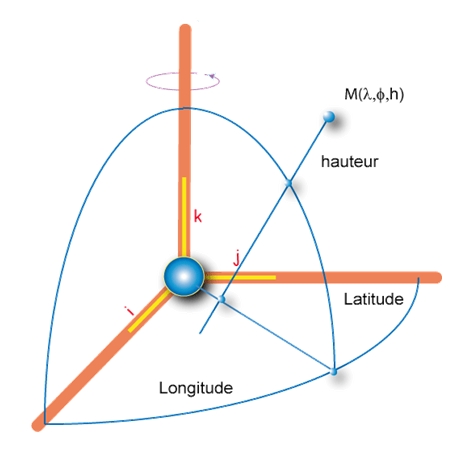
coordonnées géographiques
Coordonnées géographiques
A un repère de référence est associé un ellipsoïde de révolution qui est un modèle mathématique de la Terre débarrassée de ses reliefs. Il s’agit approximativement d’une sphère aplatie aux pôles. L’ellipsoïde est centré en O. Son axe de révolution selon le petit axe de l’ellipse méridienne est OZ. Les coordonnées géographiques tridimensionnelles sont associées à l’ellipsoïde.
- λ : longitude géodésique
- φ : latitude géodésique
- h : hauteur au dessus de l’ellipsoïde
Coordonnées planes
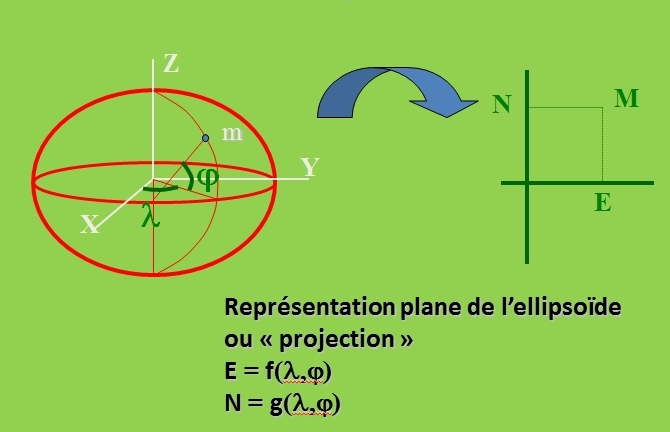
La représentation plane
Les coordonnées planes sont utilisées sur les cartes et les plans, dont la réalisation nécessite un système de projection cartographique. Chaque point de la surface terrestre est d’abord projeté sur l’ellipsoïde selon la direction normale. Puis l’ellipsoïde est transformé en surface plane. Les coordonnées associées à cette surface plane sont des coordonnées cartésiennes bidimensionnelles :
- E (Easting) pour l'abscisse
- N (Northing) pour l'ordonnée
On les calcule en fonction de la longitude λ et de la latitude φ.
Ces coordonnées sont également appelées cordonnées en projection ou coordonnées cartographiques.
A noter : en topographie ou cartographie, ces coordonnées sont usuellement notées X et Y.
En savoir plus :
Réalisation d'un repère de référence terrestreRéalisations de l’ITRS (en anglais)
Groupe de travail des références terrestres (en anglais)
Quelle est la différence entre le méridien de Greenwich et le méridien de Paris ?
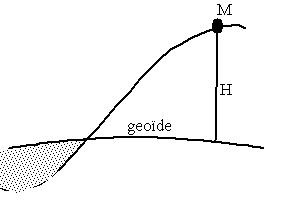
Distance entre le géoïde et le point M
Système de référence verticale et altitude
L'altitude d'un point de la surface topographique est, de manière très approchée, la distance entre le point et une surface de référence appelée géoïde.
Le géoïde est une équipotentielle du champ de pesanteur (W=Wo) qui correspond approximativement au niveau moyen des mers.
Plus rigoureusement l'altitude est définie par :
H(M) = 1 / γ . Σ g.dh
γ : valeur moyenne conventionnelle de la pesanteur
(l'expression de γ définit le type d'altitude : dynamique, orthométrique ou normale)
Σ g.dh : quantité de travail pour aller du géoïde au point M
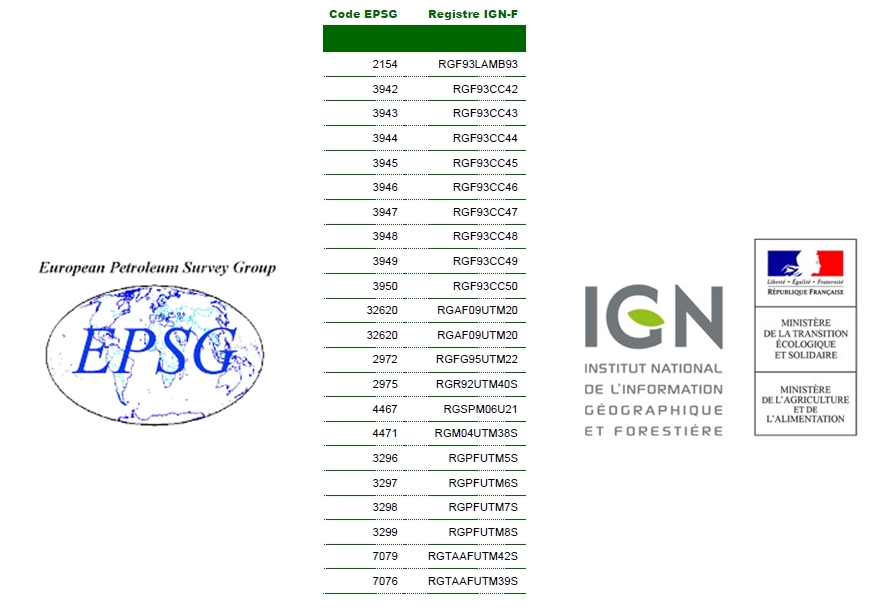
Les registres de systèmes de coordonnées
Un système de référence verticale est défini par :
Un point fondamental, souvent proche d'un marégraphe, auquel on a attribué une altitude conventionnelle, d'un type précis :
cote géopotentielle, altitude dynamique, altitude orthométrique, altitude normale.
Chaque réalisation physique du système donne lieu a un 'repère de référence vertical' constitué d'un ensemble de points physiques avec une altitude et des coordonnées. La réalisation de ce système se fait par technique de nivellement, en mesurant des dénivelées et en déterminant de proche en proche l’altitude de repères de nivellement qui constituent le réseau. On mesure aussi partiellement sur le réseau la valeur de la pesanteur par gravimétrie afin de calculer des différences de potentiel.
Exemples :
Systèmes : IGN69, IGN78, EVRS,...
Repères de référence verticale : NGF, REUN95, NIREF
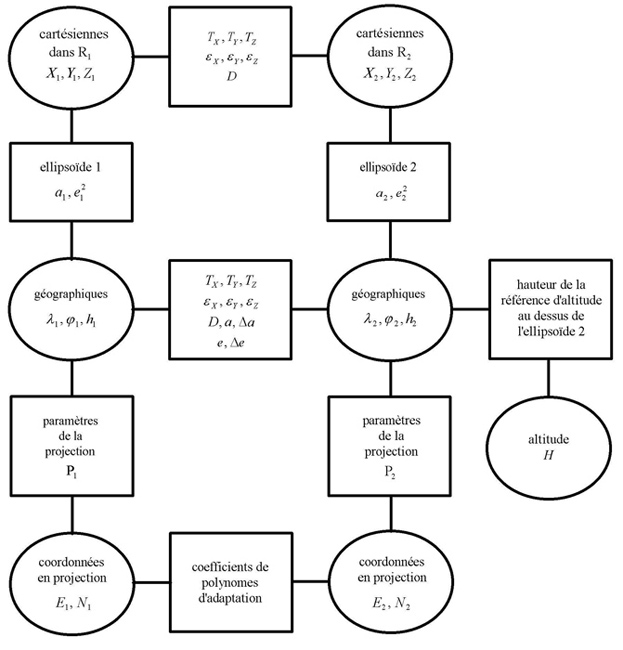
Diagramme des transformations de coordonnées
Système de coordonnées (CRS)
Il existe :
- De nombreux repères de référence dont les origines peuvent être à plusieurs centaines de mètres les uns des autres( NTF, ED50, RGF93,...)
- De nombreux ellipsoïdesdont les dimensions peuvent différer de plusieurs centaines de mètres (Clarke 1880, HAYFORD1909, IAG-GRS80,...)
- De nombreux représentations planes(UTM, Lambert-93, Conique Conforme 9 zones, Lambert Azimuthal Equal Area) ...
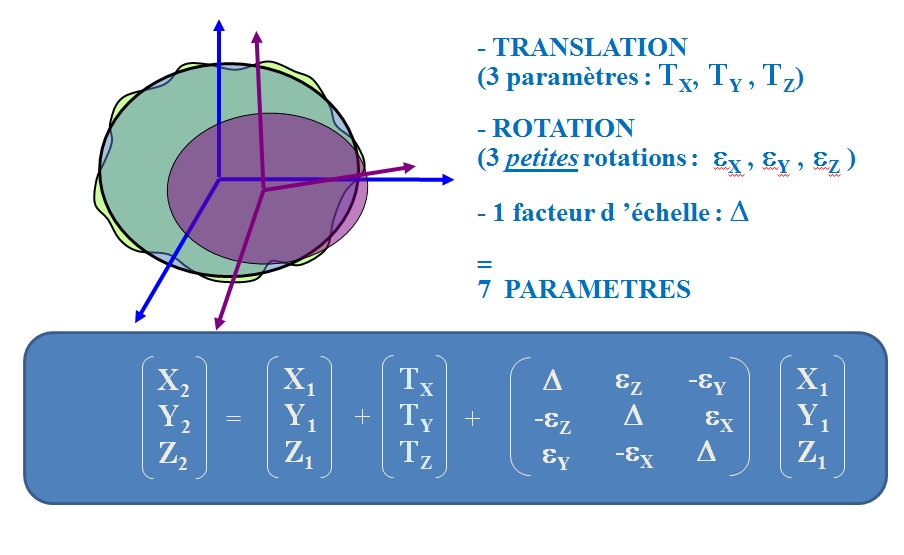
Transformation à 7 paramètres
Pour identifier un jeu de coordonnées, on utilise des systèmes de référence de coordonnées (CRS: Coordinate Reference System) qui, selon le type de coordonnées, précisent les éléments de définition nécessaires. Ces CRS sont définis dans des registres géodésiques, maintenus par différents organismes étatiques ou internationaux.
Registres de système de coordonnées
Transformation de coordonnées
 Si il s'agit du passage simple d'un type de coordonnées à un autre dans le même repère de référence, on parle de 'conversion' de coordonnées. (verticalement dans le diagramme ci-contre)
Si il s'agit du passage simple d'un type de coordonnées à un autre dans le même repère de référence, on parle de 'conversion' de coordonnées. (verticalement dans le diagramme ci-contre)
Mais, si un changement de système est nécessaire (horizontalement dans le diagramme), des paramètres de transformation doivent alors être utilisés.
Il existe des logiciels, tels que Circé, qui effectuent les transformations de coordonnées.
Pour en savoir plus sur les transformations de coordonnées en pratique : les ressources
Mis à jour le 12/09/2023