IGN

Aspects scientifiques

Surfaces de référence

En plus de l'ellipsoïde, qui est un modèle mathématique de la Terre, la géodésie traite de surfaces de référence liées au champ de pesanteur : le géoïde, le quasi-géoïde et leurs différentes réalisations.

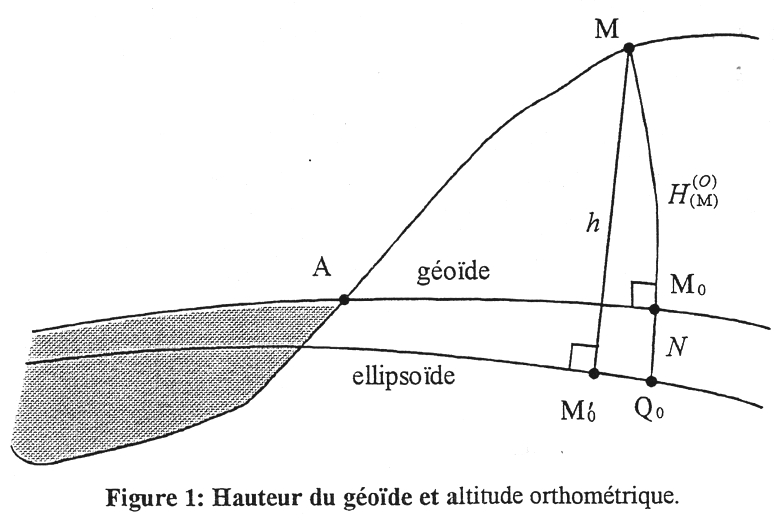
figure 1 : Hauteur du géoïde et altitude orthométrique

Le géoïde est la surface du potentiel de pesanteur terrestre qui coïncide au mieux avec le niveau moyen de la mer. Si on appelle W le potentiel et W₀ le potentiel sur le géoïde, le géoïde est caractérisé par l'équation : W = W₀.
Cette équation définit idéalement le géoïde mais ne le réalise pas pour autant : elle ne peut pas définir la forme du géoïde dans un système de référence géodésique donné.
La position du géoïde dans l'espace s'exprime au moyen de sa hauteur N au-dessus d'un ellipsoïde de référence géodésique (figure 1). Avec une très bonne approximation, N est la différence entre la hauteur ellipsoïdale h (comptée le long de la normale à l'ellipsoïde) et l'altitude orthométrique H₀(comptée le long de la ligne de force du champ) : N = h - H₀.

Pour définir le quasi-géoïde (figure 2), l'ellipsoïde est considéré comme une surface équipotentielle d'un modèle de champ appelé champ normal et noté U. Par convention, le potentiel normal sur l'ellipsoïde est égal au potentiel réel sur le géoïde, ce qui est décrit par la relation : U_Q0 = W₀.

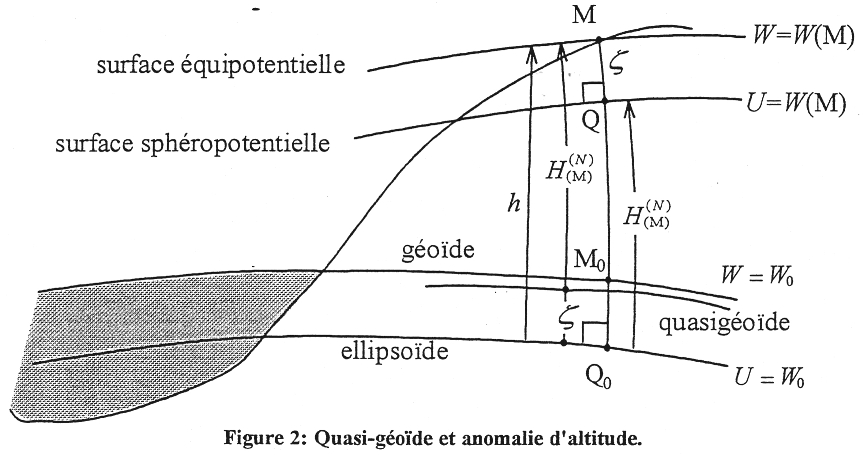
figure 2 : Quasi-géoïde et anomalie d'altitude

Par tout point M passe une surface équipotentielle du champ réel, d'équation W= W_M.
La surface de potentiel normal U égal au potentiel réel de M est appelée surface "sphéropotentielle" de M. Le point Q est l'intersection de la ligne de force du champ avec la sphéropotentielle.

H_nm est l'altitude normale du point M : c'est la distance entre l'ellipsoïde (en Q(₀) et la surface sphéropotentielle (en Q).
L'anomalie d'altitude ζ est le concept qui, dans la théorie moderne, remplace la hauteur du géoïde : c'est la distance entre la surface sphéropotentielle et la surface équipotentielle de M ; c'est aussi la hauteur du quasi-géoïde au dessus de l'ellipsoïde, ce qui définit le quasi-géoïde. On a ainsi la relation : ζ = h - H_n.

Méthodes de calcul

Le quasi-géoïde QGF98 (ellipsoïde de référence IAG-GRS80)

II existe plusieurs méthodes pour réaliser le géoïde :

• Les techniques de la géodésie spatiale (Doppler, télémétrie laser, etc.), éventuellement complétées par l'altimétrie satellitaire et la gravimétrie, permettent de calculer des coefficients d'un développement du potentiel en harmoniques sphériques. Ce développement ne doit être utilisé que dans une référence géodésique déterminée, qui n'est d'ailleurs pas toujours explicitement connue. La précision des meilleurs développements actuels est, pour la hauteur du géoïde, de quelques décimètres.


• Le nivellement astro-géodésique. Pour un ensemble de points de coordonnées géographiques géodésiques connues, on détermine les coordonnées astronomiques. Par différence, on obtient pour chaque point les composantes de la déviation de la verticale. On procède à l'intégration de ces composantes le long de chemins joignant les points deux à deux. Il faut cependant fixer arbitrairement la hauteur du géoïde en un point. La méthode a été appliquée avec succès en France avec une précision de l'ordre de 1 mètre en plaine et de 3 mètres en haute montagne. La précision peut être très nettement améliorée par apport d'information topographique. Le système de référence géodésique dans lequel le géoïde est réalisé est celui dans lequel les coordonnées géodésiques sont exprimées.


• La méthode gravimétrique, due à Stokes, consiste à intégrer des anomalies de pesanteur. Cette méthode et ses développements récents (retrait-restauration, Molodenski) sont au coeur des travaux du LAREG et du SGM mais les principes n'en sont pas exposés plus en détail dans cette page. Le géoïde est réalisé dans le système de référence du modèle de champ utilisé. Suivant les techniques de calcul, les données et le relief, la précision peut être centimétrique ou décimétrique.


• L'association de techniques spatiales (en particulier du système GPS) et de nivellement de précision conduit, par différence entre hauteur ellipsoïdale et altitude, à une réalisation point par point du géoïde ou d'une surface qui en est très proche, suivant le type d'altitude (orthométrique, normale, etc.). Le géoïde obtenu est alors réalisé dans le système de référence dans lequel sont exprimées les coordonnées des points GPS. Le géoïde n'est pas défini par son potentiel comme dans l'équation W = W₀, mais par le point origine du réseau de nivellement. D'autre part, la surface de référence d'altitude matérialisée par le réseau de nivellement (surface d'altitude nulle), qui devrait théoriquement coïncider avec le géoïde ou le quasi-géoïde, s'en écarte en raison des erreurs affectant le réseau de nivellement.


• Lorsque l'on souhaite déterminer un géoïde à partir de plusieurs types de données (par exemple un modèle global de champ préexistant, des données gravimétriques, des valeurs de déviation de la verticale, des points spatiaux nivelés, etc.), la collocation est théoriquement une bonne méthode : elle permet de traiter les différents types de données dans un modèle physique, mathématique et statistique unique et cohérent. Mais des études menées à l'IGN ont montré que, d'une part, une importante puissance de calcul lui était nécessaire et, d'autre part, sauf en modifiant les programmes disponibles de manière significative, il était difficile de traiter les problèmes de certains systématismes et, par voie de conséquence, des références géodésiques et altimétriques.

Une réalisation numérique du géoïde ou du quasi-géoïde dépend du système de référence géodésique sous-jacent, des données utilisées (types, exactitude, précision, étendue géographique, etc.), et des méthodes de traitement mises en oeuvre. Il en résulte que, pour une réalisation donnée, il existe des spécifications d'utilisation bien précises.
Par exemple, il n'est pas licite d'utiliser sans précaution un géoïde gravimétrique ou un modèle global de champ pour convertir des hauteurs ellipsoïdales en altitudes. C'est la raison pour laquelle, dans le cadre des travaux réalisés par Henri Duquenne, deux réalisations distinctes sont présentées ci-dessous :

• le quasi-géoïde gravimétrique QGF98, utilisable pour satisfaire certains besoins scientifiques. Ce quasi-géoïde est aujourd'hui remplacé par le QGF16 (calculé en 2016)
• la grille RAF98 qui matérialisait jusqu'en 2009 la référence d'altitude du Nivellement Général de la France (réseau NGF-IGN69) dans le système de référence géodésique RGF93. Cette grille, utilisable pour les opérations de nivellement par GPS dans des conditions spécifiques, est toutefois remplacée actuellement par la grille la plus récente : RAF20.

Les méthodes de réalisation du quasi-géoïde sont très proches, dans leur principe, de celles décrites pour le géoïde. Il faut cependant noter que, théoriquement, il est possible de calculer exactement l'anomalie d'altitude et, donc, le quasi-géoïde, sans hypothèses sur la masse volumique de la croûte. Il n'en est pas de même pour le géoïde, pour lequel la réduction des mesures au niveau zéro et le retrait du terrain sont nécessaires.
D'un point de vue pratique, un géoïde s'adapte mieux aux besoins d'un pays dont le type d'altitude est orthométrique. Le quasi-géoïde est plus intéressant si le type d'altitude est normal, comme c'est le cas en France.

Surface de conversion des altitudes

Ces traitements permettent l'évaluation de la précision du géoïde gravimétrique par comparaison aux points géodésiques et la réalisation de grilles de conversion des hauteurs ellipsoïdales en altitudes.

Comparaison du quasi-géoïde QGF98 aux points nivelés du RBF

Le tableau ci-contre fait l'inventaire des principales sources d'écarts entre une réalisation gravimétrique du quasi-géoïde telle que QGF98 et une référence d'altitude matérialisée par un ensemble de points spatiaux nivelés.

La seconde colonne indique un ordre de grandeur de la longueur d'onde (pour les erreurs périodiques) ou de la distance de corrélation (pour les erreurs aléatoires). Celle-ci est la distance pour laquelle la covariance entre écarts relatifs à deux points est égale à la moitié de la variance de l'écart. Si cette distance est significativement plus petite que la distance moyenne entre les points, la corrélation des écarts entre points voisins est faible.
Ces longueurs d'onde ou distances de corrélation sont importantes car certaines causes d'écarts ont une signature particulière : par exemple, les fautes de rattachement altimétrique (hauteur d'antenne GPS au dessus d'un repère...) ont une distance de covariance nulle, ce qui permet de les séparer des autres sources d'écarts.
Il est possible de modéliser les écarts dont la longueur d'onde ou la distance de corrélation est nettement plus grande que la taille de la zone d'étude (1000 kilomètres, dans notre cas) par une régression linéaire, avec :

• λ et φ désignent les coordonnées géographiques d'un point géodésique nivelé.
• λ₀ et φ₀ sont les coordonnées moyennes de la zone
• a, b, c sont trois paramètres à déterminer
• ζ est la hauteur du quasi-géoïde gravimétrique
• ζ¹ est l'anomalie d'altitude déduite d'une technique spatiale (GPS...) et du nivellement
• v est un résidu

On obtient la relation d'observation :

a + b (φ - φ₀ ) + c (λ - λ₀ ) cosφ - (ζ¹ - ζ) = v

la fonction linéaire a + b (φ - φ₀ ) + c (λ - λ₀ ) cosφ modélise :

• les écarts liés aux problèmes de systèmes de références géodésiques
• les erreurs à très grande longueur d'onde du modèle de champ
• les parties constantes et à grande distance de corrélation des erreurs du réseau de nivellement

Les résidus représentent la partie à courte longueur d'onde des erreurs du modèle de champ, ainsi que les parties à courte distance de corrélation ou non corrélées des autres erreurs.

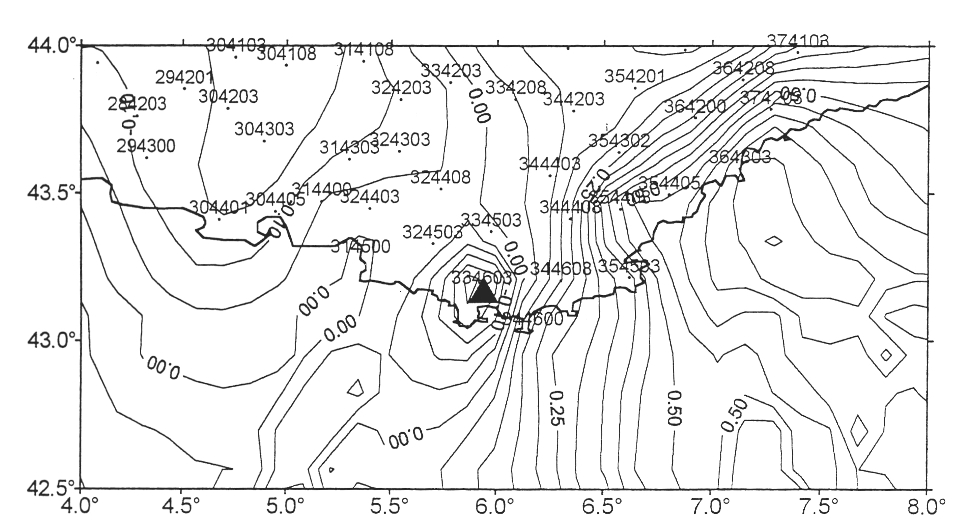
Figure 3 : Régression linéaire.

Le processus de régression s'accompagne d'une détection des fautes participant à la validation du RBF. En effet, un déplacement fortuit de repère de nivellement ou une faute de mesure entraîne sur le point en cause un résidu non-corrélé avec ceux des points voisins.
Un exemple complexe, apparu lors de la comparaison du QGF96 (le prédécesseur du QGF98) dans la région de Toulon, est donné figure 3 : des résidus positifs sont manifestement corrélés, (probablement dus à un défaut important de la gravimétrie en mer) et un résidu négatif est isolé (correspondant vraisemblablement à une faute).

L'écart-type des résidus est un indicateur global de précision du quasi-géoïde et de l'altimétrie du réseau géodésique (nivellement et GPS), sans qu'il soit possible de distinguer entre les différentes sources d'erreurs.

Réalisation de la grille de référence d'altitudes RAF20

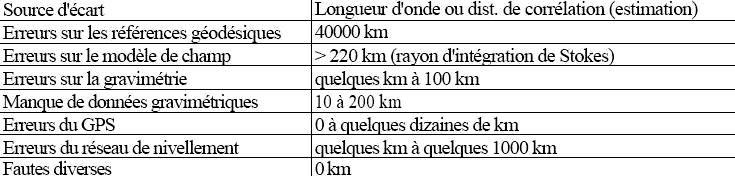
Tableau 1 : Cause d'écarts entre quasi-géoïde et référence d'altitude réalisée par un réseau

Comme le laisse prévoir le tableau 1 et comme peut le confirmer la représentation en courbe de niveau, les résidus présentent une distance de covariance assez courte. Ils sont en fait les témoins de systématismes locaux qu'il est nécessaire de gommer pour utiliser le quasi-géoïde comme référence d'altitude dans des opérations de nivellement par GPS. On propose donc de corriger le quasi-géoïde gravimétrique de la tendance générale estimée à travers les paramètres a, b, c de la régression linéaire, et d'une correction résiduelle provenant de l'interpolation par collocation des résidus.
Cette méthode très empirique ne fait qu'exploiter au mieux les propriétés statistiques des résidus, sans préjuger de leurs causes. Elle est cependant efficace si le géoïde gravimétrique est localement précis. Après la régression linéaire et le calcul des résidus, trois étapes sont nécessaires pour réaliser la grille de référence d'altitude :

Représentation en courbes de niveaux de RAF20

1. calcul de la distance de covariance, à partir de la courbe de covariance moyenne en fonction de la distance des points
2. interpolation des résidus sur les noeuds de la grille du quasi-géoïde
3. correction du quasi-géoïde

L'adaptation suivant cette méthode du quasi-géoïde QGF16 (calculé par le SGM en 2016) aux points GPS nivelés (altitudes exprimées dans le NGF-IGN69) a permis de produire des surfaces de conversion des altitudes pour la France Métropolitaine continentale. La plus récente est RAF20 (Références des Altitudes Françaises 2020) qui fait suite aux grilles RAF18 et RAF18b. Cette surface de conversion est intégrée au logiciel Circé Service Public.

A Saint-Pierre-et-Miquelon, l'adaptation du géoïde canadien#g CGG2013a (Canadian Gravimetric Geoid 2013 version a) aux points GPS nivelés a permis de produire la surface de conversion des altitudes RASPM2018, intégrée au logiciel Circé Service Public.

Aux Antilles Françaises, l'adaptation du quasi-géoïde QGAF2015 aux points GPS nivelés a permis de produire des surfaces de conversion des altitudes pour la Martinique et pour chacune des îles de l'archipel de Guadeloup, surfaces intégrées au logiciel Circé Service Public.

Sur l'île de la Réunion, l'adaptation du quasi-géoïde QGGR06 aux points GPS nivelés a permis de produire la surface de conversion des altitudes RAR07, intégrée au logiciel Circé Service Public.

Descriptif technique du quasi-géoïde QGF16 (pour la France métropolitaine continentale)

Descriptif technique de la surface de conversion RAF20 (pour la France métropolitaine continentale)

Descriptifs du quasi-géoïde QGF98 et des grilles de conversion altimétrique RAF98 et RAF09 sur la France métropolitaine

Descriptif technique du quasi-géoïde#x QGGR06 pour la Réunion